[수학] 선형대수: 벡터와 행렬

티스토리 뷰

Learn/수학

[수학] 선형대수: 벡터와 행렬

앤오엔 2022. 2. 8. 11:24

선형대수

벡터와 행렬의 특성과 관계, 연산에 대한 학문, 컴퓨터 비전과 인공지능 분야에 많이 사용됨

벡터

벡터: 숫자의 나열로 이루어진 자료형, 순서에도 의미가 있음
n차원 벡터: 원소 개수가 n인 벡터

행벡터

$x=[x_1, x_2, ..., x_n], x_{i}\in \mathbb{R}$

(벡터의 원소는 실수에 속한다고 가정)

열벡터

$x=\begin{bmatrix} x_1\\ x_2\\ ...\\ x_n\\\end{bmatrix}$

벡터의 연산

더하기

$\begin{bmatrix} 1\\ 2\\ 3\\\end{bmatrix}+\begin{bmatrix} 4\\ 5\\ 6\\\end{bmatrix} =\begin{bmatrix} 1+4\\ 2+5\\ 3+6\\\end{bmatrix} =\begin{bmatrix} 5\\ 7\\ 9\\\end{bmatrix}$

차원과 방향이 동일해야 함

스칼라 곱

$2\begin{bmatrix} 1\\ 2\\ 3\\\end{bmatrix} =\begin{bmatrix} 2\times 1\\ 2\times 2\\ 2\times 3\\\end{bmatrix} =\begin{bmatrix} 2\\ 4\\ 6\\\end{bmatrix}$

스칼라: 하나의 값을 가지는 수

내적

$\begin{bmatrix} 1\\ 2\\ 3\\\end{bmatrix} =\begin{bmatrix} 4\\ 5\\ 6\\\end{bmatrix} =1\times4+ 2\times5+3\times6 = 32$

벡터의 각 원소를 곱하고 그 합을 구하는 연산

전치

$\begin{bmatrix} 1\\ 2\\ 3\\\end{bmatrix}^{T} = \begin{bmatrix} 1& 2 & 3 \\\end{bmatrix}or\begin{bmatrix} 1& 2 & 3 \\\end{bmatrix}^{T} = \begin{bmatrix} 1\\ 2\\ 3\\\end{bmatrix}$

행벡터/열벡터를 열벡터/행벡터로 변환

행렬

행렬: mXn 형태의 행과 열로 이루어진 자료형

행렬의 연산

더하기

스칼라 곱

스칼라: 하나의 값을 가지는 수

행렬의 곱

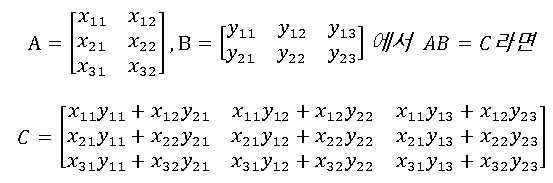
출처: 놀기 적당한 장소: 행렬(matrix) (get1ucky.blogspot.com)

왼쪽 행렬 열의 개수와 오른쪽 행렬 행의 개수가 같아야 함
교환법칙 성립되지 않으므로 순서 중요

성분곱

행렬 각 위치의 원소를 곱하는 연산
행렬 크기가 같아야 함

여러가지 행렬

정사각행렬

행과 열의 수가 같은 행렬

삼각행렬

주대각선: 정사각행렬의 왼쪽부터 오른쪽 아래로 이어지는 대각선
주대각선을 기준으로 어느 한쪽이 모두 0인 행렬

대각행렬

주대각선을 제외한 모든 원소가 0인 행렬

단위행렬

대각행렬에서 주대각선의 모든 원소가 1인 행렬
행렬 A와 단위행렬을 곱하면 행렬 A가 나옴

전치행렬

주대각선을 기준으로 행렬을 뒤집는 행렬

대칭행렬

원래 행렬과 전치행렬이 동일한 행렬

역행렬

$f(x)=y \rightarrow x=f^{-1}(y)$

의 연산을 할 때 사용

행렬식 : ad - bc
행렬식이 0이 되면 역행렬을 구할 수 없음
가역행렬: 역행렬이 존재하는 행렬
비가역행렬: 역행렬이 존재하지 않는 행렬

벡터와 연립방정식

선형방적식: 다항방정식 중 각 변수의 차수가 1인 항들의 합으로 이루어진 방정식

컨볼루션 연산

합성곱 연산이라고도 불림
2D 컨볼루션의 계산
예. 가우시안 필터 (이미지 흐리게), 소벨 필터(이미지 외곽선 따기)

※ 엘리스《프로그래밍 수학》를 듣고 이해한 바를 정리한 것으로, 사실과 다른 부분이 있을 수 있음.

저작자표시 비영리 변경금지

'Learn > 수학' 카테고리의 다른 글

[머신러닝] 선형대수학 기초 - 스칼라, 벡터, 행렬 (0)	2022.02.14
[수학] 확률과 통계: 경우의 수와 확률 (0)	2022.02.08
[수학] 수열: 수학적 귀납법 (0)	2022.02.08

기록 모음

티스토리 뷰